Partial Contour Matching

基于轮廓点夹角的方法

Riemenschneider(2010)提出了一种基于形状的物体识别方法，该方法将图像中的曲线段和模板轮廓线进行匹配，就用到了部分匹配的方法。

轮廓片段的描述

文章采用的曲线描述方式来自作者更早的工作(Donoser,2009)，该工作用于描述和比较完整闭合轮廓。而(Riemenschneider,2010)则将描述稍作改进，用于描述非闭合曲线。

一个形状的轮廓曲线（或者图像中的非闭合曲线）首先要等距采样为一个点序列 $B=\{b_1,b_2,\cdots,b_M\}$ . 然后用一个矩阵描述每三个点之间的夹角。这是一个 $M\times M$ 的矩阵，其中的元素定义如下。 $a_{ij}=\left\{\begin{array}{ll} \angle b_i b_j b_{j-\Delta}& \textrm{if } i<j-\Delta \\ \angle b_i b_j b_{j+\Delta}& \textrm{if } i>j+\Delta \\ 0& \textrm{otherwise} \end{array}\right.$ 下图就是一个示意图，显示了定义角度的两种不同情况。

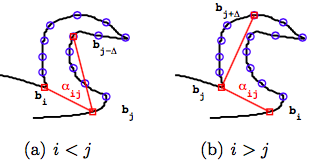
角度组成的矩阵就可以描述轮廓片段的特征。下面是一些基本的轮廓元素对应的矩阵。其中，第一行是(Donoser,2009)的矩阵；第二行是(Riemenschneider,2010)改进后的矩阵。根据矩阵元素的定义，这种描述轮廓片段的方式天然的具有平移和旋转不变性，但是没有尺度不变形。后续的匹配和识别算法要在多个尺度上进行。该矩阵的另一个特点是，通过沿着对角线进行移位，可以解决闭合轮廓在采样为点序列时起始位置选择的问题。

匹配算法

首先定义匹配。两条曲线的某一部分相匹配，就是对应的角度矩阵中沿着对角线的两个子矩阵差异比较小。下图比较了一把合拢的剪刀和一把张开的剪刀的轮廓曲线，可以明显看到四组对应的子矩阵。

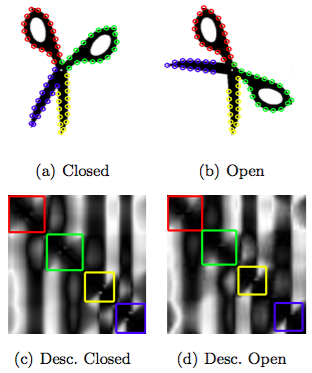
形式化的定义如下， $A_1$ 和 $A_2$ 是两条曲线对应的描述矩阵，下面定义了从 $A_1$ 上的r点开始的长度l的片段和从 $A_2$ 上的q点开始的长度为l的片段的差异度。 $D(r,q,l)=\frac{1}{l^2}\sum_{i=0}^{l-1}\sum_{j=0}^{l-1}\left[A_1(r+i,r+j)-A_2(q+i,q+j)\right]^2$ 我们设两条曲线长度分别为M和N，不妨设M较小，那么，所有的不同的片段的差异度就构成了一个三维的张量(tensor)，或者说N个 $M\times M$ 的矩阵。因此，我们可以把D视作一个张量。

快速计算张量D，需要用到一点技巧，积分图像(integral image)，用于快速计算图像中的任意矩形区域的特征（比如矩形区域像素和）。文章(Viola,2001)详细描述了该方法。一个图像i的积分图像ii中的每一个点的值是该点左上的矩形区域内像素值的和，即 $ii(x,y)=\sum_{x'\leq x,y'\leq y}i(x',y')$ . 这样，任意的矩形区域的和可以由积分图像快速计算（常数时间）。快速计算张量D的方法是，首先计算N个不同的积分图像，分别对应于将矩阵 $A_2$ 沿着其对角线移位得到的N个不同的矩阵和矩阵 $A_1$ 的差值的积分图像。有了这N个积分图像，就可以快速计算张量D了。

在张量D的基础上，进一步筛选长度和相似度符合要求的匹配。为此，定义如下的函数。 $\mathcal{L}(r,q,l)=\left\{\begin{array}{ll} l&\textrm{if }D(r,q,l)\leq d_{lim}\textrm{ and } l\geq l_{lim}\\ 0&\textrm{otherwise} \end{array}\right.$ 进一步将这个函数转化为2元函数， $\Psi(r,q)=\max_l \mathcal{L}(r,q,l)$ ，就可以求得该函数的局部极大值，这些局部极大值就对应于一些满足长度和相似度要求的匹配。

识别物体：假设投票

在上面的匹配过程中，假设曲线A1是模板(reference)，曲线A2是测试图像中的曲线(query)。那么，得到的每一对匹配就表示模板有可能出现在图像之中，并且可以估计出现的位置，这就构成了一个假设，于是可以用大量匹配进行假设投票。投票的结果就是物体识别的结果。

在(Donoser,2009)中，作者采用了另外的方法进行形状提取。与物体识别不同，形状提取不需要考虑背景线条的影响，也不考虑线条可能会破碎。形状提取需要考虑的主要因素是，两个形状在多大程度上相似。对于存在差异的两个形状，对比的局部越小，差异度就越小；对比的局部越大，差异度就越大。作者的方法遵循了这样的观点，在(Bronstein,2009)中，对部分相似性进行了形式化的定义和计算。

参考文献

Riemenschneider, H., Donoser, M., & Bischof, H. (2010). Using partial edge contour matches for efficient object category localization. In ECCV 2010.
Donoser, M., Riemenschneider, H., & Bischof, H. (2009). Efficient partial shape matching of outer contours. In ACCV 2009.
Viola, P., & Jones, M. (2001). Rapid object detection using a boosted cascade of simple features. In CVPR 2001.
Bronstein, A. M., Bronstein, M. M., Bruckstein, A. M., & Kimmel, R. (2009). Partial similarity of objects, or how to compare a centaur to a horse. IJCV, 84(2), 163-183.