String Algorithms
字符串通常实现为一个可随机访问的线性表,简单来说,就是数组。
C的字符串表示以'\0'结尾。
字符串的算法通常涉及动态规划。
前缀树(Trie)和KMP算法
Trie是存储和快速查找有限个字符串的一种数据结构,相当于一个树形的自动机。 根节点表示空字符串,从根出发到某一节点的路径表示一个字符串, 字符串由该路径经过的边所对应的字符连接而成。 在Trie树中加入后缀连接(suffix link),可以构成一个Trie图。 Trie图也是一个自动机,状态转换图为有向无环图(DAG), 可以用于查找一个有限字典中的单词是否在某一字符串中出现。 Trie图是KMP算法的推广形式,将查找一个单词推广为查找一个有限字典中的任意词。
KMP算法
KMP算法在长度为n的目标字符串str中查找长度为m的模式字符串pattern,
平凡的方法是在str中的逐个位置对齐pattern进行比较,复杂度为O(mn)。
KMP算法提供一种当比较出错时,在str上不回退的快速比较方法,
方法的关键是确定pattern重新对齐的位置,重新对齐的位置与出错位置构成后缀关系。
比如,模式串是"ababc",当比较到"abab..."时,发现后续字符不是"c",
那么应该把模式串对齐到"ab..."继续比较。
因此,需要构建数组t[i],使得t[i]=max{k|pattern[0...k-1]==pattern[i-k...i-1]},
那么,在比较到位置i出错时,就可以从位置t[i]开始继续比较。
kmp_table(pattern[])
t[0] = -1, t[1] = 0, i = 2
p = 0 // 始终有pattern[0...p-1]==pattern[i-1-p...i-2]
while (i < pattern.length)
if (pattern[i-1] == pattern[p]) then
p++, t[i] = p, i++
else if (p > 0) then
p = t[p]
else
t[i] = 0, i++
end-if
end-while
return t
kmp_search(str[], pattern[])
t = kmp_table(pattern), i = 0, p = 0
while (i + p < str.length)
if (pattern[p] == str[i+p]) then
if (p == pattern.length - 1) then return i
p++
else if (t[p] >= 0) then
i += p - t[p], p = t[p]
else
i++, p = 0
end-if
end-while
return -1 // not found
Trie树和Trie图
Trie图将KMP推广到了有限个模式串的情形。 下面是一个Trie树(图片来自wiki,请忽略数字)。
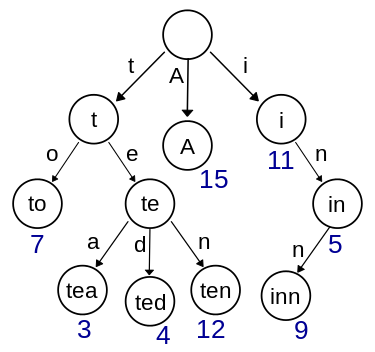
Trie树就像是原始的pattern,当发生匹配错误时,只能从树的根部重新开始匹配。
Trie图的优化方法是,在每个节点添加next表,
存储在节点对应的状态遇到任何字符时应该采取的状态转换。
这个next表可以从根部开始逐层构造,这个表使得Trie图成为一个确定性有限自动机(DFA)。
构造next表需要借助后缀指针(suffix_link),即指向该节点的后缀节点的指针。
一个节点的后缀节点所代表的串,是该节点的串的后缀。
trie_graph(trie)
queue.push(trie.root)
while (!queue.empty)
p = queue.pop()
if (p == trie.root || p.parent == trie.root) then
p.suffix_link = trie.root
else
c = p.char // p所在路径上的最后一个字符
p.suffix_link = p.parent.suffix_link.next[p.char]
end-if
for c in character-set // 对字母表中每一字符
if (p.next[c] != null) then
queue.push(p.next[c])
else if (p == trie.root) then
p.next[c] = trie.root
else
p.next[c] = p.suffix_link.next[c]
end-if
end-for
end-while
这个构造算法可以看做在树上逐层进行的动态规划算法。
其中的suffix_link可以理解为KMP算法中所构造的数组。
后缀数组
将一个字符串的所有后缀按照字典序排列,得到的就是后缀数组。
设suffix(i)表示从i开始的后缀,后缀数组有两种表示形式:
sa[i]表示suffix(sa[i])的字典序为i,即按照后缀的字典序存储了后缀开始位置;rank[i]表示suffix(i)的字典序为rank[i],即存储了不同开始位置的后缀的字典序。
后缀数组可以通过深度优先遍历后缀树得到,后缀树可以在O(n)时间构造, 因此,最优的后缀数组构造算法是线性时间的。
后缀树
后缀树是包含某一字符串的全部后缀的一个Trie。假设字符串长度为n, 后缀树要满足一下条件:
- 有n个叶子节点。为了满足该条件,可以在字符串末尾加一个特殊字符
$,这样后缀串就不会构成前缀关系。 - 除了root之外的非叶节点的孩子数量大于1,即必须分支。设非叶节点数量为x,那么根据节点总度数和边的关系;因此非叶节点数量小于等于n-1,节点总数小于2n。
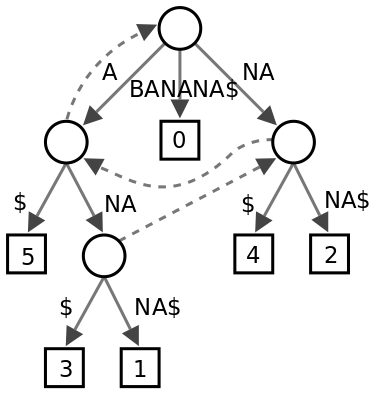
构建后缀树的朴素方法需要平方的时间复杂度。 Ukkonen给出了一个O(nlogn)的算法(Ukkonen,1995)。 Farach给出了一个O(n)的算法(Farach,1997)。
参考文献
- Ukkonen, E. (1995), "On-line construction of suffix trees", Algorithmica 14 (3): 249–260.
- Farach, Martin (1997), "Optimal Suffix Tree Construction with Large Alphabets", 38th IEEE Symposium on Foundations of Computer Science (FOCS '97), pp. 137–143.