Suffix Tree

专门开一篇来写后缀树，因为它用途比较广泛，但是构造算法有一点麻烦。

Ukkonen算法

Esko Ukkonen是芬兰赫尔辛基大学的教授，他在1995年给出了这一算法(Ukkonen,1995)。 算法的特点是能够由左至右的为一个字符串构造后缀树，即算法是在线的。

后缀树是一棵压缩的suffix trie。Trie是一种树形的自动机。 文中约定了一些符号表示方法。

• 【字符集】: 为之构建后缀树的字符串是字符集$\Sigma$上的串$T=t_1 t_2\cdots t_n$。
• 【后缀】： $T_i=t_i\cdots t_n$表示T的一个后缀；$T_{n+1}=\epsilon$是一个空后缀；字符串T的全部后缀的集合记为$\sigma(T)$。
• 【前缀】： $T^i=t_1\cdots t_i$表示T的一个前缀。
• 【STrie】：由字符串T的全部后缀构建的trie记为$STrie(T)=(Q\cup\{\perp\},root,F,g,f)$。它是一个自动机，Q是状态集合，root是初始状态，F是终结状态集合，g是状态转换函数，f是后缀链接suffix link。
• 【特殊状态】： $\perp$是一个特殊状态，它是root的后缀链接，$f(root)=\perp$；同时，它可以从任意字符转换到root状态，即$\forall a\in\Sigma,g(\perp,a)=root$。
• 【状态转换、后缀链接】： 用$\bar{x}$表示子串x所对应状态。那么如果$a\in\Sigma$，状态转换$g(\bar{x},a)=\overline{xa}$，后缀链接$f(\overline{ax})=\bar{x}$。
• 【a转换】： 如果有状态r和字符a，状态转换g(r,a)叫做一个a转换(a-transition)。
• 【STree】： 后缀树$STree(T)=(Q'\cup\{\perp\},root,g',f')$仅含有suffix trie中的显性状态，即叶节点和分支状态；其他状态叫做隐性状态。后缀链接f'仅定义在分枝状态上，而且分支状态的后缀连接也是分支状态。
• 【STree的状态转换】： 后缀树的状态转换形如g'(r,(k,p))，表示$g'(r,\overline{t_k\cdots t_p})$，压缩掉了中间的隐形状态。k叫做左指针，p叫做右指针，它们表示这个转换经过了子串$t_k\cdots t_p$。如果$t_k=a$，那么它叫做a转换。一个状态出发的a转换至多一个。
• 【规范引用】： 为了统一的表示显性状态和隐形状态，需要定义状态的规范引用(canonical reference)。一个状态r可以用一个引用对(s,w)表示，s是r的祖先，s表示的串加上w就得到r表示的串。如果s是r最近的祖先(或者就是r本身)，那么这样的引用对就是规范的(canonical)。为了节省空间，通常不直接存储w串，而是存储它在原始字符串T上的起始位置坐标，因此，引用对可以表示为(s,(k,p))。

构造suffix trie

假设已经得到了T的长度为(i-1)的前缀的suffix trie，$STrie(T^{i-1})$。 在此基础上构造$STrie(T^i)$，就是在$T^{i-1}$的每一个后缀后面添加字符$t_i$， 也就是要检查$STrie(T^{i-1})$的每一个终结状态$r\in F_{i-1}$， 如果r没有$t_i$转换，就要添加一个新的转换和一个新的状态。 所有的$r\in F_{i-1}$实际上都在一条后缀链接构成的路径上，我们称之为boundary path。 根据定义，后缀链接指向的是长度减一的后缀，这些终结状态都是$T^{i-1}$的后缀， 因此，对于任何$r\in F_{i-1}$，都有$r=f^j(\overline{t_1\cdots t_{i-1}})$， 其中，$0\le j<i$表示重复应用f的次数。 这条boundary path，就是从最深的$\overline{t_1\cdots t_{i-1}}$状态开始的后缀链接路径。

当遍历boundary path的时候，遇到第一个有$t_i$转换的状态就可以立即停止。 因为根据suffix trie的定义，如果$\bar{x}$状态存在，那么x的任何子串对应的状态都存在， 于是，遍历就不需要继续进行了。 而且，我们确定这个遍历一定会停止，因为$\perp$状态有全部字符的转换。

于是，从$STrie(T^{i-1})$构造$STrie(T^i)$可以按照如下算法进行（沿着boundary path添加新状态）。 用这个算法构造suffix trie的复杂度显然跟suffix trie的状态总数是线性关系的，即O(|Q|)。

Algorithm 1: extend_suffix_trie
  r = state of t[1...i-1]
  while (g(r,t[i]) is undefined)
    g(r,t[i]) = r1 = new state
    if (oldr1 is defined) then f(oldr1) = r1
    oldr1 = r1
    r = f(r)
  end-while
  f(oldr1) = g(r,t[i])

构造suffix tree

设boundary path上的状态依次为$s_1=\overline{t_1\cdots t_{i-1}},s_2,\cdots,s_i=root,s_{i+1}=\perp$。 设j是boundary path上遇到的第一个非叶节点， 设j'是boundary path上遇到的第一个具有$t_i$转换的状态， 那么称$s_j$为active point，称$s_{j'}$为end point。 在active point之前， 算法1给每个叶子节点创建了一个后继， 这在路径压缩过的后缀树里面并不增加新的状态，而是改变既有的转换。 假设之前的转换是g'(s,(k,i-1))=r，那么新的转换就是g'(s,(k,i))=r，更新这些转换其实并不必要。 在后缀树中，所有到叶节点的转换都是开放转换(open transition)， 转换的右指针总是指向字符串结尾，可以表示为$g'(s,(k,\infty))=r$。 采用这样的表示，就不需要更新active point之前的任何状态转换。

这样一来，构造后缀树只需要考虑从active point到end point的状态， 然而，这些状态并不总是显性状态， 因此不存在一条简单的由后缀链接构成的boundary path。 对于显性状态或者隐形状态，我们统一用规范引用对(canonical reference pair)来表示。 在遍历boundary path的时候，沿着引用对中的显性状态的后缀链接进行。 假设(s,(k,i-1))是$STree(T^{i-1})$的boundary path上的一个状态， 那么下一个状态应该是(f'(s),(k,i-1))，我们需要将这个引用对规范化。

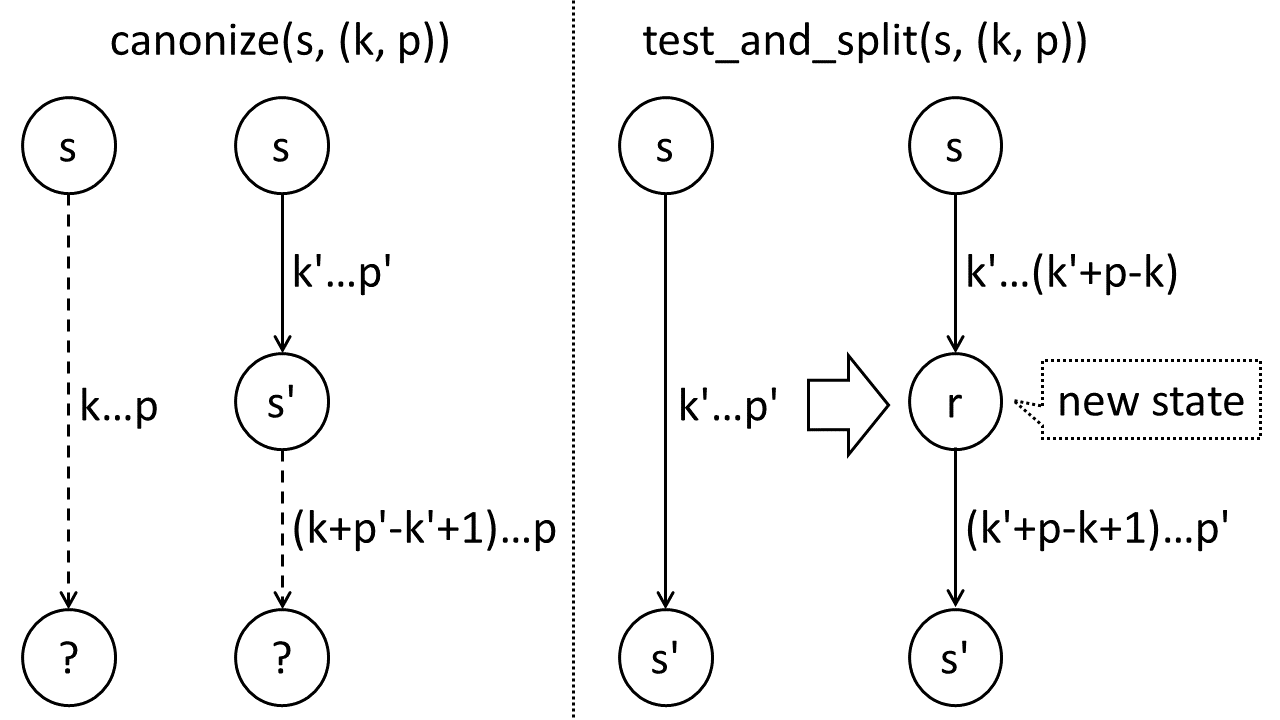
canonize(s,(k,p))
  while (k <= p)
    find t[k] transition g'(s,(k',p')=s'
    if (p'-k' > p-k) then break
    k=k+p'-k'+1, s=s'
  return (s,k)

有了canonize函数，就可以沿着显性状态的后缀链接遍历boundary path，得到一系列的规范引用。 然后，需要判定是否为end point，如果不是end point，则需要增加新的状态。 下面的函数检查规范引用(s,(k,p))代表的状态是否有t转换。

test_and_split(s,(k,p),t)
  if (k > p) then //该状态为s本身
    if (s has t-transition) then return (true,s)
    return (false,s)
  else //该状态为隐性状态
    find t[k] transition g'(s,(k',p'))=s'
    if (t[k'+p-k+1] == t) then return (true,s)
    create new state r
    replace the t[k] transition with g'(s,(k',k'+p-k))=r
    add transition g'(r,(k'+p-k+1,p'))=s'
    return (false,r)
  end-if

有了上面两个函数，就可以用类似构造suffix trie的方式来构造后缀树。 下面假设$STree(T^{i-1})$已经构造好了，要加入第i个字符$t_i$， 下面的函数从active point (s,(k,i))开始遍历boundary path。 遍历到end point结束，然后返回$STree(T^i)$上的active point(实际就是当前end point的后继，因为之前的添加的状态都是叶节点)。

update(s,(k,i))
  repeat
    (is_end_point,r) = test_and_split(s,(k,i-1),t[i])
    if (is_end_point) then break
    create new state r'
    add transition g'(r,(i,INF))=r'
    if (oldr is defined) then f'(oldr) = r
    oldr = r
    (s,k) = canonize(f'(s),(k,i-1))
  end-repeat
  if (oldr is defined) then f'(oldr) = s
  return (s,k)

最后，Ukkonen算法构造后缀树的过程如下。 我们用top表示状态$\perp$。

Algorithm 2: Ukkonen
  t = t[1...n] + '#'
  create state root and top
  add transition g'(top,(-1,-1))=root for any character a
  f'(root)=top
  s = root, k = 1, i = 1
  while (t[i] != '#')
    (s,k) = update(s,(k,i))
    (s,k) = canonize(s,(k,i))
    i = i + 1
  end-while

参考文献

1. Ukkonen, E. (1995), "On-line construction of suffix trees", Algorithmica 14 (3): 249–260.
2. Farach, Martin (1997), "Optimal Suffix Tree Construction with Large Alphabets", 38th IEEE Symposium on Foundations of Computer Science (FOCS '97), pp. 137–143.